重点考点一:线性方程和函数
本场考试中线性方程和函数依然是非常高频考点的考点。具体考点包括斜率,两直线平行或垂直的性质,线性方程求解等。
高频词汇考察:
slope 斜率
constant 常数
Integer 整数
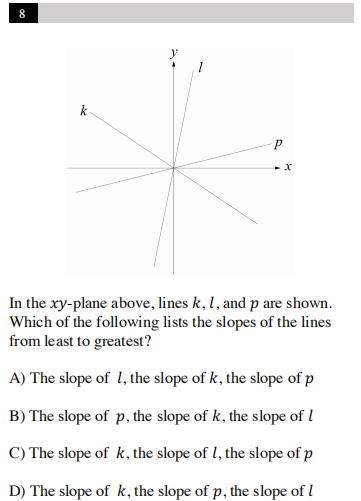
例题1 非计算器部分第8题
具体考点:结合图像判断斜率正负大小。
答案:D
解析:设直线k, l, p斜率分别为k1, k2, k3,由图可得,k1<0,k2>k3>0,所以k1<k3<k2.
例题2 非计算器部分第10题
具体考点:斜率的性质。
答案:B
解析:斜率为0,则直线与x轴平行。仅直线y=1符合条件。

例题3 非计算器部分第17题
具体考点:斜率的性质。
答案:9
解析:因为x任意值满足方程,所以等式左右两直线平行(该题情况下两直线重合)。两直线平行,则斜率相等。可求k值为9。

例题4 非计算器部分第2题
具体考点:线性方程组的实际应用
答案:A
解析:通过方程解决实际问题也是线性函数类高频考点。先明确变量含义,再根据表述列出相应方程组即可。

重点考点二:二次函数
本考点主要考察解一元二次方程,函数的各种性质(开口方向,对称轴,顶点坐标,解的个数等)和表达式,韦达定理等。
高频词汇考察:
Parabola 二次函数
Vertex 顶点
Intersection point 交点
例题1 非计算器部分第12题
具体考点:二次方程的解
答案:D
解析:令h(x)= 0,即2(x- 4)2- 32= 0,解得x= 0或8。所以t值为8.

例题2 非计算器部分第30题
具体考点:二次方程的表达式
答案:A
解析:根据顶点坐标且抛物线与x轴有两个交点,得出抛物线开口向下,则y=-ax2+bx+c中a>0;根据顶点坐标(3,1)列出顶点式y=-a(x-3)2+1,化为一般式可得y=-ax2+6ax-9a+1;a>0,则c=-9a+1<1,仅c值为-8满足条件。

例题3 非计算器部分第32题
具体考点:一元二次方程求解
令两函数相等,求解交点坐标,得到交点y坐标值即为答案。
答案:1
解析:令(x-1)2= 2x-3,解得交点坐标为(2,1),所以y值为1.

例题4 非计算器部分第34题
具体考点:一元二次方程根的判别式
答案:7或8或13
解析:方程有2个整数解,则可对原方程进行因式分解,化为(x-3)(x-4)=0或(x-2)(x-6)=0或(x-1)(x-12)=0满足条件,且a>0,则a值为7或8或13.
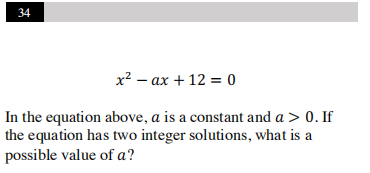
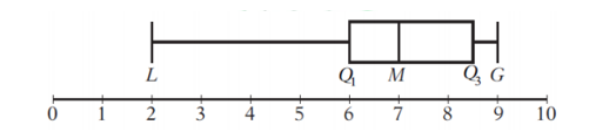
重点考点三:统计学之箱线图
统计学中最近出现了以前不太常考的“箱线图”这一新的考点,且考频越来越高,本场考试中就考察了2道。箱线图(Boxplot)也称箱须图(Box-whisker Plot),是利用数据中的五个统计量:最小值、四分位数、中位数、第三四分位数与大幅值来描述数据的一种方法,它也可以粗略地看出数据是否具有有对称性,分布的分散程度等信息。如下图所示,L表示最小值,G表示大幅值,Q1为个4分位数,M为中位数,Q3为第三个四分位数。
高频词汇考察:
Median 中位数
Mean 平均数
Range 极差
例题1 非计算器部分第1题
具体考点:箱线图
答案:B
解析:考察箱线图读图能力,方框中间分割线标记中位数,所以中位数约为7000.

例题2 非计算器部分第27题
具体考点:箱线图
答案:D
解析:考察箱线图读图能力,由图可知最小值为37,大幅值为87,个四分位数为51,中位数为61,第三个四分位数为84;所以极差range=50.

以上是2019年5月亚太SAT数学考情分析,数学考试部分较为薄弱的同学可以有的放矢,查漏补缺,结合知识点做针对性练习,争取冲击高分。